Absorption of RF Radiation

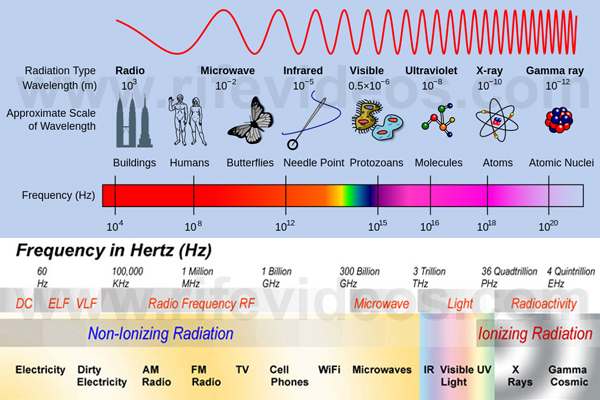
How does RF radiation interact with human tissue?

RF Radiation should not be confused with X-ray radiation because they are not the same band of frequencies. Dr. Rife's Machines output radio-frequency waves from below the AM radio band up to about 20 MHz (20 Megahertz or 20 million cycles per second). The FM radio band is at 100 MHz. Below is a chart that shows the different wavelength bands. Notice the X-ray band is way higher than the Radio Frequency band.

A radio wave in space is characterized by its frequency, intensity of electric and magnetic fields, direction, and polarization. The interaction of external radio waves with biological bodies produces internal electric and magnetic fields, which can be calculated by solving Maxwell's equations for the given boundary conditions. This becomes a complex problem, however, because biological bodies are heterogeneous and complex in shape, making an exact solution impossible. In addition, the intensity of the internal field is greatly dependent on the boundary conditions under which the external field is applied. The frequency, intensity, and polarization of the field, in addition to the size, shape, dielectric properties of the exposed body, the spatial configuration of the exposure source and the body, and the presence of other objects in the vicinity, play a big role in the effect the radio waves will have on the body. For this reason, the internal field created in a mouse under a given external field will be much different than the internal field created in a man under the same external field.

We are interested in how external fields couple with biological bodies to create internal fields. The field strength inside a cell nucleus, for example, would be needed to judge any effects on genetic information. Likewise, the field strength across the cell membrane would be needed to evaluate possible membrane excitation phenomena. So we must first be able to figure out the field strength inside the human body and then how this is related to membrane potentials etc.

Internal field strength increases proportionally with the external field strength, but the internal field is not necessarily uniform even if the incident field is uniform.

Exact field strength is dependent on local geometry: in a man standing in a field perpendicular to the ground, the average current density in the legs is greater than in the trunk, by a factor that corresponds to the ratio of the cross sectional areas of the trunk and leg. Absorbed energy depends on the size of the body, curvature of its surface, ratio of body size to wavelength, and the source characteristics.

How do different tissues absorb radiation?

The magnetic permeability of most tissues is practically equal to that of free space, meaning that tissue is essentially nonmagnetic. Interactions at high radio frequencies occur through the electric field, which therefore describes the exposure field interactions with the tissue. Frequency characteristics, modulation characteristics, and modulation frequency of the external field are also important in determining interactions with tissue.

Both electric (E) and magnetic (H) fields at radio frequencies decrease exponentially with distance from the boundary of a tissue because of energy dissipation after reflection W. Penetration depth is defined as the distance in which the power density decreases by a factor of e^-2 (13.5 percent), and is a function of frequency and tissue properties. At higher frequencies, fields penetrate much less than at lower frequencies. For example, at 2.45 GHz (microwave oven frequency), penetration depth in tissue is about 2.0 cm, while at 10 GHz, it is about 0.4 cm. At higher frequencies, any heating that occurs is primarily surface heating. Penetration depth for fat and bone is nearly five times greater than for higher-water-content tissues. At frequencies between 300 and 3000 MHz, electromagnetic energy can penetrate into more deeply situated tissues, making it especially desirable for therapeutic applications.

Two properties of a tissue that determine how electromagnetic radiation is absorbed are permittivity and conductivity. The permittivity of a tissue is a strong function of frequency, generally decreasing with increased frequency. The whole-body averaged value permittivity is approximately 2/3 that of muscle tissue.

If the relative permittivity of the object is very close to one, very little scattering occurs. When an object is very small compared to the wavelength of the incident field, very little scattering occurs. When the size of the object is comparable to or larger than a wavelength, significant scattering occurs.

The conductivity of tissue is essentially that of its intra and extracellular fluids. In general, the wetter a material is, the more lossy it is, and the drier, the less lossy. We see this daily in the that a wet paper placed in a microwave oven will get hot only as long as it is wet, after which it will no longer absorb energy and not be heated. Muscle and high-water content tissues will absorb more than drier tissues such as fat and bone.

The time-averaged rate of energy absorption for steady-state sinusoidal fields per unit volume (W /m³) at a point inside an absorber is P = sE² where is E is the root-mean-squared magnitude of the electric field vector at that point inside the material, and s is the conductivity. The dielectric properties of all tissues are tabulated in reference 1 p. 92ff.

How much radiation does an antenna give off?

The expected value of S (absorption) in W/m² with an antenna with gain G, receiving an input power P, at a distance r, is giving by S = PG/4(pi)r², where PG = ERP (effective radiated power). S is also known as the Poynting Vector. Gain is a measure of the ability to direct RF power in specific directions in comparison to an isotropic antenna, and generally specified in the far-field. In the near field gain may vary, which may be an issue in determining exposure limits.

If antennas are propagating efficiently, there should be no field at the base of the antenna.

What is Specific Absorption Rate (SAR)?

Because the nature of the interactions between biological tissue and external radio waves is so complex, studies are done either through simplified theoretical models or experiments. Of course the usefulness of these studies depends on the accuracy of the models and the instruments used to make measurements. Measurement of internal fields, however, is not possible in humans, and has only been done in animals. In order to determine hazardous exposure levels for man, it is therefore necessary to measure external fields. External fields which are dangerous for man are determined by measuring levels of harmful internal fields created in animals and then extrapolating to determine the corresponding external field that would cause that same specific absorption rate (SAR) in man.

How is SAR defined?

Specific Absorption Rate (SAR) is the time derivative of the incremental energy (dW) absorbed by, or dissipated in an incremental mass (dm) contained in a volume element (dV) of a given density (r).

SAR= (1/r)( dW /dt)

where dW/dt is the rate of change of the energy per unit volume of charged particles at that point. The SAR is therefore expressed in watts per kilogram (W /kg).

Average SAR (or whole-body average SAR) is defined as the ratio of the total power absorbed in the exposed body to its mass, whereas the local SAR is the value within a defined unit volume or mass, which can be arbitrarily small.

The SAR does not fully characterize the internal fields created (e.g. it does not account for interactions directly through the H field or orientation of the E fields created), but it is a useful unit of measurement in dosimetric studies. For example, because knowing SAR gives a measure of the internal fields, which could possibly cause effects other than direct heating.

How is SAR measured?

The rate of temperature change of tissue in vivo is related to SAR by:
Delta(T)/Delta(t) = (SAR + Pm - Pc - Pb)/C
where Delta(T) is the temperature increase,
Delta(t) is the exposure duration,
Pm the metabolic heating rate,
Pc is the rate of heat loss per unit volume due to thermal conduction,
Pb the rate of heat loss per unit volume due to blood flow,
and C is the specific heat of the tissue.

For short periods of exposure, this can be approximated as Delta(T)/Delta(t) = (SAR)/C because presumably a steady-state existed before exposure and Pm - Pc - Pb = O. Measurements of SAR are often made using this formula because of its simplicity. Because the temperature must be linear with time, the fields must be intense enough that the temperature rise is not influenced significantly by heat transfer. Because there may be interaction between a thermometer and the field, new methods are being used to measure temperatures, such as thermography which uses an infrared meter to measure temperature over the entire surface.

Does SAR depend on orientation?

Yes. There are three possible orientations to an electromagnetic wave:

E-polarization: the electric field is parallel to the major axis, cross-section of body perpendicular to the incident magnetic field is larger.
H-polarization: the electric field is perpendicular to the major axis, the magnetic field vector is parallel to the major axis and cross-section is smaller
K-polarization: both electric and magnetic field vectors are perpendicular to the major axis.

In general, E-polarization produces the highest energy absorption for frequencies up to and slightly beyond the resonance region. This is because coupling between the body and the electric field is maximized in this orientation. This is due to the antenna-like properties of the body.

To be even more specific, the human body is an ellipsoid, not a spheroid, and hence has six polarizations, but these can be approximated by the three orientations listed above.

What is the effect of a ground plane on SAR?

A person standing on a perfectly conducting ground plane (link to glossary) with E polarization experiences a resonant frequency approximately one-half that in free space, because the ground plane makes the individual appear about twice as tall electrically. Resonance frequency is then about 40 MHz.

How does SAR depend on size, shape and frequency?

The frequency of maximal absorption is called the resonance frequency (for humans it is between 70 and 100 MHz), and depends on orientation with respect to the incident field. In general, the rule is that the shorter the subject, the higher the resonance frequency, and vice versa.

For maximum energy coupling (E-polarization defined above), the long-axis of the body is oriented in direction of the electric field vector, i.e. the incident plane wave is perpendicular to the body. The resonance frequency generally occurs at a frequency for which the length of the body is about one half of a free-space wavelength. Below resonance, SAR is intermediate for K polarization, and least for H polarization. For frequencies such that the ratio of the longest body dimension (L) to the free space wavelength (1) is less than 0.2, the average SAR depends on frequency as f^2. The average absorption then goes through a resonance in the region where 0.2 < L/1 < 1.0. The average SAR increases to a maximum near L/l = 0.4 and then decreases as 1/f.
When L/1 > 1.0, whole-body absorption decreases slightly but approaches the geometrical optics limit of about one half of the incident power asymptotically. Source: NCRP Report No. 119

This resonant absorption length of 0.4 lambda agrees with results from antenna analysis. So for L = 175cm, maximum absorption occurs at about lambda = L/O.4 = 437.5cm which is a frequency of 68.6 Mhz.

SAR is higher when the body is more perpendicular than parallel to an incident field. It is also higher when the cross section of the body perpendicular to the incident magnetic field is larger. So for E polarization SAR increases as an object becomes longer and thinner, and decreases as it becomes shorter and fatter.

Average SAR is highest at 0.25 W/kg at 70 MHz for humans for an incident power density of 10 W/m²; at this frequency the average SAR for a rat is only 0.0125 W/kg. Average SAR is highest at 0.8 W/kg at 700 MHz for rats; for humans at this frequency, the SAR is less than 0.04 W/kg. It is thus crucial to take into account the body size and frequency of the external field to establish relationships between biological effects that occur in lab animals and the corresponding effects that might occur in humans at a given incident power density.

What is the difference between the far field and the near field?

The far field extends from a minimum distance of approximately 2D2/1, where D is the larger dimension of the antenna and 1 is the wavelength. In this region the electromagnetic field has a mostly plane-wave character, meaning that the E-field and H-field vectors are perpendicular, and are both also perpendicular to the direction of propagation. The magnitude of the E and H fields is equal in the far field, so only one of the two needs to be measured. Power density varies inversely as the square of the distance from the antenna. For RF exposure measurements in some types of antenna systems, the extent of the near-field is considerably less. For circular parabolic antennas, for example, the distance may be closer to 0.35D2/1.

In the near field, however, power density has an oscillatory dependence on distance from the antenna. Objects placed near the source of the field may have a strong effect on the nature of the field, a fact that becomes especially important in trying to obtain measurements. The far field can be approximated as a spherical wave, that can in turn be approximated by a plane wave described below.

Spherical Wave: The wave fronts are spheres and propagate radially outward, with the magnitude of E and H varying as 1/r, where r is the distance from the source. Otherwise similar to plane waves at large r.
Plane wave: True plane waves do not exist, but serve as a good model for waves in the far field. The wave fronts are planes, and E and H and the direction of propagation are mutually perpendicular. For free space E/H = 377 ohms, and E and H are constant in any plane perpendicular to the direction of propagation.

How are external electric fields measured?

Because it is difficult and impractical to measure internal electric fields, in general we must measure external fields and base exposure limits on these.

Broadband instruments/survey meters are frequency independent sensitivity and measure integrated intensity of fields, with no frequency spectrum information.

Narrowband instruments (e.g. spectrum analyzer) are selective and provide information about field intensity at a selected frequency.

Personal Dosimeter attempts - the goal of such a device would be to measure the exposure of a person throughout their daily activities. The dosimeter is only capable of recording cumulative radiation, meaning the power density integrated over time. Biological effects are dependent on the dose rate, and not just on total dose (i.e. exposure to 200 m W /cm² for 10 min is not the same as exposure to 1 mW/cm² for 2000 min). The dosimeter is also partially shielded by the wearer.

Measurement of internal fields is difficult, but can be done with non-perturbing implantable probes. We can then get the SAR if we the conductivity of material is known, and then only at a few points.

Interference with other objects near the antenna, scattering or reflecting surfaces modulation characteristics of the radiation are important, accuracy of instruments, pulse shape and duration, and repetition rate.

For an example of external measurements, see the measurements taken in Newton and Arlington.

What are analytical and numerical models of human body absorption?

As an alternative to experimental methods, several different kinds of models can be used to predict SAR and heating effects. These include using finite element methods, Fourier transforms, convolution methods, and simplified spheroid models to make predictions without needing laboratory tests. Many of these models have shown very accurate results.

Scientific Report: Harvard Education Courses 1997.